Medan dalam ilmu fisika adalah kehadiran besaran fisika di setiap titik dalam ruang (atau, secara lebih umum, ruang-waktu). Kekuatan medan biasanya berubah-ubah dalam suatu wilayah.
Teori Medan biasanya mengacu pada konstruksi dinamika suatu medan, yaitu spesifikasi bagaimana suatu medan berubah terhadap waktu atau terhadap komponen lain dari medan tersebut.
1. Vektor
Pengertian vektor
Vektor merupakan suatu besaran yang mempunyai besar dan arah.
Contoh: kecepatan, percepatan, gaya, momentum, medan magnet, medan listrik
Notasi Vektor
- Ruas garis berarah yg panjang dan arahnya tertentu.
- Vektor dinyatakan dg huruf ū, u, u (bold), atau u (italic).
- Jika u menyatakan ruas garis berarah dari A ke B, maka ditulis dengan lambang u = AB
- Notasi u dibaca “vektor u”
Vektor sbg pasangan bilangan
u = (a,b), dimana a : komponen mendatar, b : komponen vertikal
Vektor sbg kombinasi vektor satuan i dan j
u = ai + bj
Panjang vektor u ditentukan oleh rumus
Aljabar vektor
Definisi-definisi yang mendasar pada vektor adalah sebagai berikut:
- Duah buah vektor A dan B sama jika memiliki besar dan arah yang sama
- Sebuah vektor yang besarnya sama dengan vektor A, tetapi berlawanan arah dengan vektor A dinyatakan dengan vektor -A
Penjumlahan vektor
- Penjumlahan vektor menurut aturan segitiga dan aturan jajaran genjang:
- Dalam bentuk pasangan sebagai berikut:
Elemen identitas
- Penjumlahan vektor menurut aturan segitiga dan aturan jajaran genjang:
- Dalam bentuk pasangan sebagai berikut:
Elemen identitas
- Vektor nol ditulis 0
- Vektor nol disebut elemen identitas
- u + 0 = 0 + u = u
- Jika u adalah sebarang vektor bukan nol, maka –u adalah invers aditif u yang didefinisikan sebagai vektor yang memiliki besar sama tetapi arah berlawanan.
- u – u = u + (-u) = 0
Pengurangan vektor
- Selisih dua vektor u dan v ditulis u – v didefinisikan u + (-v)
Pengurangan vektor
- Selisih dua vektor u dan v ditulis u – v didefinisikan u + (-v)
- Dalam bentuk pasangan bilangan
Perkalian vektor dan skalar
- mu adalah suatu vektor dg panjang m kali panjang vektor u dan searah dengan u jika m > 0, dan berlawanan arah jika m < 0.
Sifat-sifat operasi vektor
Perkalian vektor dan skalar
- mu adalah suatu vektor dg panjang m kali panjang vektor u dan searah dengan u jika m > 0, dan berlawanan arah jika m < 0.
Sifat-sifat operasi vektor
- Komutatif à a + b = b + a
- Asosiatif à (a+b)+c = a+(b+c)
- Elemen identitas terhadap penjumlahan
- Sifat tertutup-> hasil penjumlahan vektor juga berupa vektor
- Ketidaksamaan segitiga |u+v| ≤ |u| + |v|
- 1u = u
- 0u = 0, m0 = 0.
- Jika mu = 0, maka m=0 atau u = 0
- (mn)u = m(nu)
- |mu| = |m||u|
- (-mu) = - (mu) = m (-u)
- Distributif : (m+n)u = mu + nu
- Distributif : m(u+v) = mu + mv
- u+(-1)u = u + (-u) = 0
Hasil Penjumlahan dan pengurangan vektor
Menghitung Besar Vektor Hasil Penjumlahan dan Pengurangan
Menentukan Arah Vektor Hasil Penjumlahan dan Pengurangan
- u+(-1)u = u + (-u) = 0
Hasil Penjumlahan dan pengurangan vektor
Menghitung Besar Vektor Hasil Penjumlahan dan Pengurangan
Menentukan Arah Vektor Hasil Penjumlahan dan Pengurangan
- Perkalian titik (dot product) a•b (dibaca a dot b) antara dua vektor a dan b merupakan
perkalian antara panjang vektor dan cosinus sudut antara keduanya.
- Dalam bentuk komponen vektor, bila a = [a1,b1,c1] dan b = [a2,b2,c2], maka :
- a•b > 0 jika {γ| 0 < γ < 90o}
- a•b = 0 jika {γ| γ = 90o}
- a•b < 0 jika {γ| 90o < γ< 180o}
Vektor Ortogonal
- Teorema
Hasil perkalian dot product antara dua vektor bukan-nol adalah nol jika dan
hanya jika vektor-vektor tersebut saling tegak lurus
- Vektor a disebut ortogonal thd vektor b jika a•b = 0, dan vektor b juga ortogonal thd
vektor a.
- Vektor nol 0 ortogonal terhadap semua vektor.
- Untuk vektor bukan-nol
a•b = 0 jika dan hanya jika cos γ = 0 à γ = 90o = π/2
Besar dan Arah dalam Perkalian Dot Product
Besar Sudut γ dapat dihitung dengan:
example:
answer:
Vektor moment (m) tegak lurus thd bidang roda (sumbu z negatif ).
2. Gaya Coulomb
( 1736 - 1806 )
Pengertian Gaya Coulomb
Gaya Coulomb adalah gaya listrik yang timbul antara benda-benda yang bermuatan listrik.
Perumusan Hukum Coulomb
Besarnya gaya tarik menarik atau tolak menolak antara dua muatan listrik sebanding dengan besar masing-masing muatan dan berbanding terbalik dengan kuadrat jarak kedua muatan.
Jika benda A memiliki muatan q1 dan benda B memiliki muatan q2 dan benda A dan benda B berjarak r satu sama lain, gaya listrik yang timbul di antara kedua muatan tersebut dapat dituliskan sebagai berikut
Dimana: F adalah gaya listrik atau gaya coulomb dalam satuan newton k adalah konstanta kesebandingan yang besarnya 9 x 109 N m2 C–2 muatan q dihitung dalam satuan coulomb (C)
dengan ε0 adalah permitivitas ruang hampa yang besarnya 8,85 x 10–12 C2 N–1 m–2
Notasi vektor
Dalam notasi vektor, hukum Coloumb dapat dituliskan sebagai berikut:
yang dibaca sebagai gaya yang dialami oleh muatan q1q2. Untuk gaya yang dialami oleh muatan q2 akibat adanya muatan q1 dituliskan dengan menukarkan indeks  , atau melalui hukum ketiga Newton dapat dituliskan akibat adanya muatan
, atau melalui hukum ketiga Newton dapat dituliskan akibat adanya muatan
Gaya listrik merupakan besaran vektor sehingga operasi penjumlahan antara dua gaya atau lebih harus menggunakan konsep vektor, yaitu sesuai dengan arah dari masing-masing gaya. Secara umum, penjumlahan vektor atau resultan dari dua gaya listrik F1 dan F2 adalah sebagai berikut.
- untuk dua gaya yang searah maka resultan gaya sama dengan penjumlahan dari kedua gaya tersebut. Adapun, untuk dua gaya yang saling berlawanan, resultan gaya sama dengan selisih dari kedua gaya
(gambar)
R = F1 + F2 dan R = F1 – F2
2. untuk dua gaya yang saling tegak lurus, besar resultan gayanya adalah
3 untuk dua gaya yang membentuk sudut θ satu sama lain, resultan gayanya dituliskan sebagai berikut
Untuk penjumlahan lebih dari dua gaya, perhitungannya dapat menggunakan metode analiti.
Pengertian listrik
Sebuah muatan listrik dikatakan memiliki medan listrik di sekitarnya. Medan listrik adalah daerah di sekitar benda bermuatan listrik yang masih mengalami gaya listrik. Jika muatan lain berada di dalam medan listrik dari sebuah benda bermuatan listrik, muatan tersebut akan mengalami gaya listrik berupa gaya tarik atau gaya tolak.
Medan listrik adalah efek yang ditimbulkan oleh keberadaan muatan listrik, seperti elektron, ion, atau proton, dalam ruangan yang ada di sekitarnya. Medan listrik memiliki satuan N/C atau dibaca Newton/coulomb
kuat medan listrik adalah vektor gaya Coulomb yang bekerja pada satu satuan muatan yang kita letakkan pada suatu titik dalam medan gaya ini, dan dinyatakan dengan
Contoh medan listrik yang timbul dari muatan listrik q1 dan q2
3. Kuat Mendan
Pengertian listrik
Sebuah muatan listrik dikatakan memiliki medan listrik di sekitarnya. Medan listrik adalah daerah di sekitar benda bermuatan listrik yang masih mengalami gaya listrik. Jika muatan lain berada di dalam medan listrik dari sebuah benda bermuatan listrik, muatan tersebut akan mengalami gaya listrik berupa gaya tarik atau gaya tolak.
Medan listrik adalah efek yang ditimbulkan oleh keberadaan muatan listrik, seperti elektron, ion, atau proton, dalam ruangan yang ada di sekitarnya. Medan listrik memiliki satuan N/C atau dibaca Newton/coulomb
kuat medan listrik adalah vektor gaya Coulomb yang bekerja pada satu satuan muatan yang kita letakkan pada suatu titik dalam medan gaya ini, dan dinyatakan dengan
Contoh medan listrik yang timbul dari muatan listrik q1 dan q2
Asal medan listrik
Rumus matematika untuk medan listrik dapat diturunkan melalui Hukum Coulomb, yaitu gaya antara dua titik muatan: Menurut persamaan ini, gaya pada salah satu titik muatan berbanding lurus dengan besar muatannya. Medan listrik didefinisikan sebagai suatu konstan perbandingan antara muatan dan gaya[1]:
Maka, medan listrik bergantung pada posisi. Suatu medan, merupakan sebuah vektor yang bergantung pada vektor lainnya. Medan listrik dapat dianggap sebagai gradien dari potensial listrik. Jika beberapa muatan yang disebarkan menghasiklan potensial listrik, gradien potensial listrik dapat ditentukan.
 akibat adanya sebuah titik muatan
akibat adanya sebuah titik muatan  yang terletak di
yang terletak di  digunakan rumus [4]
digunakan rumus [4]
 yang terletak di
yang terletak di  sehingga diperoleh rumus seperti telah dituliskan pada permulaan artikel ini, atau bila dituliskan kembali dalam notasi vektornya:
sehingga diperoleh rumus seperti telah dituliskan pada permulaan artikel ini, atau bila dituliskan kembali dalam notasi vektornya:
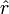

Disarankan untuk menggunakan rumusan yang melibatkan dan
dan  karena lebih umum, dan dapat diterapkan untuk kasus lebih dari satu muatan dan juga pada distribusi muatan, baik distribusi diskrit maupun kontinu. Penyederhanaan ini juga kadang membuat pemahaman dalam menghitung medan listrik menjadi agak sedikit kabur. Selain itu pula karena penyederhanaan ini hanya merupakan salah satu kasus khusus dalam perhitungan medan listrik (kasus oleh satu titik muatan di mana titik muatan diletakkan di pusat koordinat).
karena lebih umum, dan dapat diterapkan untuk kasus lebih dari satu muatan dan juga pada distribusi muatan, baik distribusi diskrit maupun kontinu. Penyederhanaan ini juga kadang membuat pemahaman dalam menghitung medan listrik menjadi agak sedikit kabur. Selain itu pula karena penyederhanaan ini hanya merupakan salah satu kasus khusus dalam perhitungan medan listrik (kasus oleh satu titik muatan di mana titik muatan diletakkan di pusat koordinat).
 diketahui, melalui perhitungan gradiennya [5]:
diketahui, melalui perhitungan gradiennya [5]:
 adalah
adalah
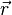 akibat adanya muatan
akibat adanya muatan  yang terletak di
yang terletak di  . Dengan demikian medan listrik di titik
. Dengan demikian medan listrik di titik 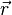 akibat seluruh muatan yang tersebar dituliskan sebagai
akibat seluruh muatan yang tersebar dituliskan sebagai
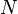 adalah jumlah titik muatan. Sebagai ilustrasi, misalnya ingin ditentukan besarnya medan listrik pada titik
adalah jumlah titik muatan. Sebagai ilustrasi, misalnya ingin ditentukan besarnya medan listrik pada titik 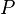 yang merupakan perpotongan kedua diagonal suatu bujursangkar bersisi
yang merupakan perpotongan kedua diagonal suatu bujursangkar bersisi  , di mana terdapat oleh empat buat muatan titik yang terletak pada titik sudut-titik sudut bujursangkar tersebut. Untuk kasus ini misalkan bahwa
, di mana terdapat oleh empat buat muatan titik yang terletak pada titik sudut-titik sudut bujursangkar tersebut. Untuk kasus ini misalkan bahwa  dan
dan  dan ambil pusat koordinat di titik
dan ambil pusat koordinat di titik  untuk memudahkan. Untuk kasus dua dimensi seperti ini, bisa dituliskan pula
untuk memudahkan. Untuk kasus dua dimensi seperti ini, bisa dituliskan pula
Untuk suatu kawat yang merentang lurus pada sumbu , pada jarak
, pada jarak  di atasnya, dengan kawat merentang dari
di atasnya, dengan kawat merentang dari 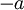 sampai
sampai 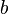 dari titik proyeksi
dari titik proyeksi 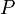 pada kawat, medan listrik di titik tersebut dapat dihitung besarnya, yaitu:
pada kawat, medan listrik di titik tersebut dapat dihitung besarnya, yaitu:
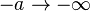 dan
dan  maka dengan menggunakan dalil L'Hospital diperoleh
maka dengan menggunakan dalil L'Hospital diperoleh
 dari kawat, dapat dituliskan medan listriknya adalah
dari kawat, dapat dituliskan medan listriknya adalah
 adalah vektor satuan radial dalam koordinat silinder:
adalah vektor satuan radial dalam koordinat silinder:
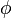 adalah sudut yang dibentuk dengan sumbu-x positif.
adalah sudut yang dibentuk dengan sumbu-x positif.
Menghitung medan listrik
Untuk menghitung medan listrik di suatu titik akibat adanya sebuah titik muatan
akibat adanya sebuah titik muatan  yang terletak di
yang terletak di  digunakan rumus [4]
digunakan rumus [4]Penyederhanaan yang kurang tepat
Umumnya untuk melakukan penyederhanaan dipilih pusat koordinat berhimpit dengan titik muatan yang terletak di
yang terletak di  sehingga diperoleh rumus seperti telah dituliskan pada permulaan artikel ini, atau bila dituliskan kembali dalam notasi vektornya:
sehingga diperoleh rumus seperti telah dituliskan pada permulaan artikel ini, atau bila dituliskan kembali dalam notasi vektornya: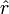

Disarankan untuk menggunakan rumusan yang melibatkan
 dan
dan  karena lebih umum, dan dapat diterapkan untuk kasus lebih dari satu muatan dan juga pada distribusi muatan, baik distribusi diskrit maupun kontinu. Penyederhanaan ini juga kadang membuat pemahaman dalam menghitung medan listrik menjadi agak sedikit kabur. Selain itu pula karena penyederhanaan ini hanya merupakan salah satu kasus khusus dalam perhitungan medan listrik (kasus oleh satu titik muatan di mana titik muatan diletakkan di pusat koordinat).
karena lebih umum, dan dapat diterapkan untuk kasus lebih dari satu muatan dan juga pada distribusi muatan, baik distribusi diskrit maupun kontinu. Penyederhanaan ini juga kadang membuat pemahaman dalam menghitung medan listrik menjadi agak sedikit kabur. Selain itu pula karena penyederhanaan ini hanya merupakan salah satu kasus khusus dalam perhitungan medan listrik (kasus oleh satu titik muatan di mana titik muatan diletakkan di pusat koordinat).Tanda muatan listrik
Muatan listrik dapat bernilai negatif, nol (tidak terdapat muatan atau jumlah satuan muatan positif dan negatif sama) dan negatif. Nilai muatan ini akan mempengaruhi perhitungan medan listrik dalam hal tandanya, yaitu positif atau negatif (atau nol). Apabila pada setiap titik di sekitar sebuah (atau beberapa) muatan dihitung medan listriknya dan digambarkan vektor-vektornya, akan terlihat garis-garis yang saling berhubungan, yang disebut sebagai garis-garis medan listrik. Tanda muatan menentukan apakah garis-garis medan listrik yang disebabkannya berasal darinya atau menuju darinya. Telah ditentukan (berdasarkan gaya yang dialami oleh muatan uji positif), bahwa
- muatan positif
(+)akan menyebabkan garis-garis medan listrik berarah dari padanya menuju keluar, - muatan negatif
(-)akan menyebabkan garis-garis medan listrik berarah menuju masuk padanya. - muatan nol
( )tidak menyebabkan adanya garis-garis medan listrik.
Gradien potensial listrik
Medan listrik dapat pula dihitung apabila suatu potensial listrik diketahui, melalui perhitungan gradiennya [5]:
diketahui, melalui perhitungan gradiennya [5]:Energi medan listrik
Medan listrik menyimpan energi. Rapat energi suatu medan listrik diberikan oleh [6] adalah permittivitas medium di mana medan listrik terdapat, dalam vakum
adalah permittivitas medium di mana medan listrik terdapat, dalam vakum 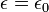 .
. adalah vektor medan listrik.
adalah vektor medan listrik.
 adalah
adalah adalah elemen diferensial volum.
adalah elemen diferensial volum.
Distribusi muatan listrik
Medan listrik tidak perlu hanya ditimbulkan oleh satu muatan listrik, melainkan dapat pula ditimbulkan oleh lebih dari satu muatan listrik, bahkan oleh distribusi muatan listrik baik yang diskrit maupun kontinu. Contoh-contoh distribusi muatan listrik misalnya:- kumpulan titik-titik muatan
- kawat panjang lurus berhingga dan tak-berhingga
- lingkaran kawat
- pelat lebar berhingga atau tak-berhingga
- cakram tipis dan cincin
- bentuk-bentuk lain
Kumpulan titik-titik muatan
Untuk titik-titik muatan yang tersebar dan berjumlah tidak terlalu banyak, medan listrik pada suatu titik (dan bukan pada salah satu titik muatan) dapat dihitung dengan menjumlahkan vektor medan listrik di titik tersebut akibat oleh masing-masing muatan. Dalam kasus ini lebih baik dituliskan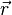 akibat adanya muatan
akibat adanya muatan  yang terletak di
yang terletak di  . Dengan demikian medan listrik di titik
. Dengan demikian medan listrik di titik 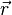 akibat seluruh muatan yang tersebar dituliskan sebagai
akibat seluruh muatan yang tersebar dituliskan sebagai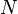 adalah jumlah titik muatan. Sebagai ilustrasi, misalnya ingin ditentukan besarnya medan listrik pada titik
adalah jumlah titik muatan. Sebagai ilustrasi, misalnya ingin ditentukan besarnya medan listrik pada titik 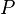 yang merupakan perpotongan kedua diagonal suatu bujursangkar bersisi
yang merupakan perpotongan kedua diagonal suatu bujursangkar bersisi  , di mana terdapat oleh empat buat muatan titik yang terletak pada titik sudut-titik sudut bujursangkar tersebut. Untuk kasus ini misalkan bahwa
, di mana terdapat oleh empat buat muatan titik yang terletak pada titik sudut-titik sudut bujursangkar tersebut. Untuk kasus ini misalkan bahwa  dan
dan  dan ambil pusat koordinat di titik
dan ambil pusat koordinat di titik  untuk memudahkan. Untuk kasus dua dimensi seperti ini, bisa dituliskan pula
untuk memudahkan. Untuk kasus dua dimensi seperti ini, bisa dituliskan pulaKawat panjang lurus
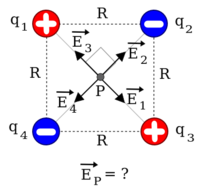
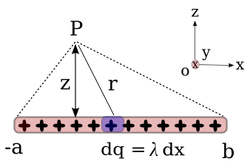
Kawat panjang lurus merupakan salah satu bentuk distribusi muatan yang menarik karena bila panjangnya diambil tak-hingga, perhitungan muatan di suatu jarak dari kawat dan terletak di tengah-tengah panjangnya, menjadi amat mudah.Untuk suatu kawat yang merentang lurus pada sumbu
 , pada jarak
, pada jarak  di atasnya, dengan kawat merentang dari
di atasnya, dengan kawat merentang dari 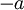 sampai
sampai 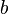 dari titik proyeksi
dari titik proyeksi 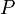 pada kawat, medan listrik di titik tersebut dapat dihitung besarnya, yaitu:
pada kawat, medan listrik di titik tersebut dapat dihitung besarnya, yaitu: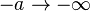 dan
dan  maka dengan menggunakan dalil L'Hospital diperoleh
maka dengan menggunakan dalil L'Hospital diperoleh dari kawat, dapat dituliskan medan listriknya adalah
dari kawat, dapat dituliskan medan listriknya adalah adalah vektor satuan radial dalam koordinat silinder:
adalah vektor satuan radial dalam koordinat silinder: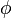 adalah sudut yang dibentuk dengan sumbu-x positif.
adalah sudut yang dibentuk dengan sumbu-x positif.



































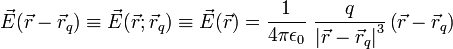
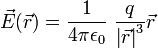













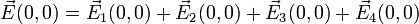

![E_z =
\frac{1}{4\pi\epsilon_0}\ \frac{\lambda}{z} \
\left[
\frac{b}{\sqrt{z^2+b^2}}
+\frac{a}{\sqrt{z^2+a^2}}
\right]](http://upload.wikimedia.org/math/e/5/c/e5c6456573df6a6c19ba66c547ba13ad.png)
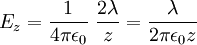


0 komentar:
Posting Komentar